Feed Sidebar
Note: watch the Feed Sidebar section of my blog for information on updates to this extension.
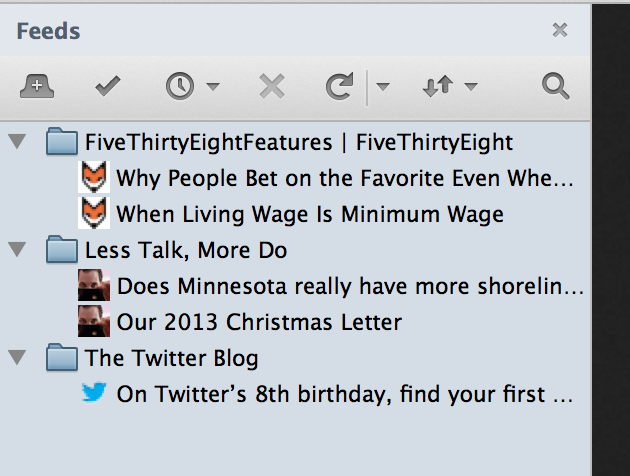
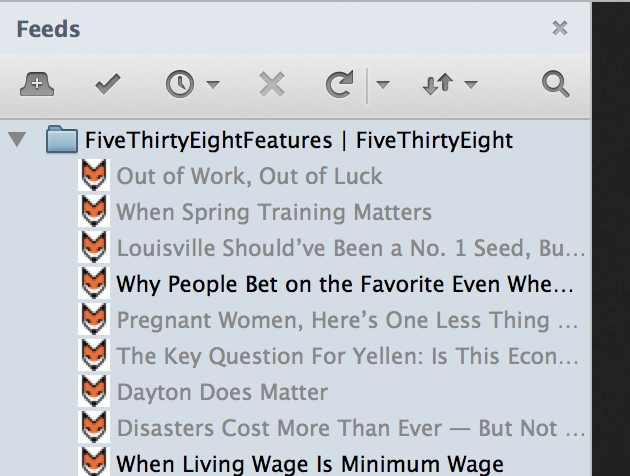
The Feed Sidebar is an extension for the Mozilla Firefox Web browser that displays the new items from your Live Bookmarks in the sidebar. It is intended to be a lightweight extension of the RSS capabilities already included in Firefox, not a completely new feed management system.
Installing the Feed Sidebar will add a new sidebar to Firefox that, when opened, will load the feeds that you have bookmarked in Firefox and display any unread items from those feeds. Clicking on an item will show a preview in the bottom of the sidebar, and double- or middle-clicking will open the item in the browser and remove it from the sidebar. The Feed Sidebar will also notify you of broken or unavailable feeds, something which I wish Firefox did in a more obvious manner:
You can choose to show items that you've already read:
You can filter your feeds with the search bar:
The toolbar buttons perform the following tasks:
- Open All in Tabs
- Mark All as Read
- Set maximum age for feed items
- Stop current update
- Reload feeds
- Change update interval (reload button dropdown)
You can access the options from the context menu:
The latest version of the Feed Sidebar is version 2.0.
If you're having trouble with the extension or would like to see a new feature added, you can:
- Contact me (@cfinke) on Twitter
- Fill out a this bug report form. (If you're requesting a new feature, just disregard any text about reproducing a bug.)
- or e-mail me at cfinke@gmail.com.
Christopher Finke is a software engineer. He is available for birthday parties and bar mitzvahs. 
June 3rd, 2007 at 3:47 pm
hello, sorry my english
is it possible to edit the time where rss is in ticker, (older than 20 days then delete)i have any rss that are from beginning 2007 and they will show anytime
June 22nd, 2007 at 9:17 am
I hope there's an option to make each feed to be initially collapsed/expanded when feed sidebar is opened.
June 23rd, 2007 at 9:43 am
is it possible to display feed titles within a part(column) of a blog instead of being directed to another page of totally different layout?
ty.
July 10th, 2007 at 4:39 am
Will you also update the add-on on the Mozilla site?
July 27th, 2007 at 4:55 am
Great extension, just what I was looking for! Thank you very much!
A tiny suggestion: to somehow be notified when there are new items available. Perhaps putting an icon and some text in the status bar?
November 1st, 2007 at 5:33 pm
Any chance you could update this to work with Firefox 3.0a9+?
November 9th, 2007 at 5:41 am
Any idea why Feed Sidebar doesn't use the name I gave the Live bookmark?
November 22nd, 2007 at 10:57 am
It would be great if the extension could display read and unread ones too, and if it could support grouping the feeds into folders (like Sage does).
December 2nd, 2007 at 8:04 pm
Great add-on apart from the fact that it relies on Firefox's browsing history which I delete after each session, therefore I see the same feeds pop up every time I load the sidebar.
Also, an icon in the status bar to alert me of new feeds would be very useful.
December 11th, 2007 at 1:27 am
Good as it is, two small changes will make it much better in my book:
(1) Keep Firefox's bookmark hierarchy instead of pulling all the feeds into a flat list. Many people like to organize and categorize their feeds in folders.
(2) Don't open all feeds by default when you start Feed Sidebar. The list becomes too long and makes navigating to a particular feed more difficult.
December 14th, 2007 at 2:00 pm
"Open All in Tabs"
is this a fucking joke?
January 2nd, 2008 at 6:47 pm
Brilliant extension.... great work :)
February 11th, 2008 at 10:45 am
Please, add a option to prefix items with [R] for the items that was read, instead of hide them.
Thanks
February 13th, 2008 at 12:23 pm
Thanks for the great extension. Just wondering if it's possible to add a confirmation dialogue to the Open All In Tabs though please as I have over 97 feeds and occasionally I click it accidentally instead of Mark All As Read and it freezes for a long while before opening an awful lot of tabs that I didn't want.
February 14th, 2008 at 7:56 am
Great extension, but i think todays update is not working, i get 'invalid elements' on all my feeds now.
Thanks again, i've been lovin' this sucker for months now.
- Luke
February 15th, 2008 at 4:54 am
OK first great extension really like it.
Some points:-
1. Get rid of the "Open all in tabs" button hit it by accident and spent the next 30 minutes being asked about different cookies.
2. the extension keep's telling me that I haven't read stories when I have. IF its going to be called Unread Feed Items on the sidebar then it should shrink with usage.
3. an option for a river of news would be great. A river of news orders everything by date rather than categorising then by the feed title. I love the show all news in the last 24 hours bit really good idea. makes up for point 2.
keep up the great work love this extension.
Ado
February 21st, 2008 at 6:16 am
For a couple of days now, I get "No Summary Provided" when selecting an article. Is this something missing in the feed or has some feature of Feed Sidebar stopped working?
February 22nd, 2008 at 4:31 pm
Hi, great extension, this has been a wonderful replacement for the old Sage RSS reader I used to use that stopped being developed some time ago and no longer works in any of the 3.0 betas. It's been a solid, fast, and highly usable extension.
Unfortunately, I do have some negative feedback for the 1.3/1.3.1 versions released this week: while I do love the new features, I've noticed the feed checking has slowed down considerably, sometimes locking up the entire browser for several minutes. I've also had a number of instances of the browser crashing when I try to mark a feed as read, and after restarting the browser, a number of feeds (which I hadn't read yet) have been arbitrarily marked as read.
I've reverted to using 1.2.2 for the time being, but would love to help support your continuing development of this extension; please feel free to email me for any further details of my particular setup, etc. if you think it will help to work out the kinks.
Thanks very much for all your work!
February 26th, 2008 at 10:39 am
I'm having the same problems as Matt -- version 1.3.1 locks up my browser every time it checks for new feeds. I've waited several minutes and then killed the Firefox process.
I'm running Firefox 2.0.0.12 on Windows Vista.
March 12th, 2008 at 2:53 am
I seem to be getting the same problem with the newest versions. Some feeds that have had updates are not showing any new news on them in the newest versions. Also Firefox 2.0.0.12 on Vista.
March 12th, 2008 at 2:54 am
Sorry, Anonymous above is me.
March 12th, 2008 at 9:10 am
Thanks for this extension.
When I wrote the comment listed with number 13, I hadn't installed the current version, and I didn't know the option to show the "read items".
Now this option allow to show "read items" with different color, and is sufficient. The request to put [R] as prefix, now it is not necessary.
Thanks
March 13th, 2008 at 4:36 pm
Could it be possible to make more visible those feeds that have new items since last visit?
In form of bolding their title and showing a number stating the amount of new entries or similar.
Thanks for your work, it's a nice extension.
March 25th, 2008 at 1:13 pm
[...] Feed Sidebar 2.0 has been released. Upgrade now to enable filtering your feeds with the search bar and to experience the big improvements in performance and memory usage. [...]
March 25th, 2008 at 6:22 pm
The extension is great! Exactly what I needed.
But why doesn't it show pictures?
March 28th, 2008 at 3:03 am
Hi thanks for the update today! They work great.
March 29th, 2008 at 11:55 pm
I like this addon!
I agree with other commenters, I would like the notion of "already read" to not be tied to the browser's history, since I also periodically delete that.
I also would like the view of my live feeds to preserve the hierarchy that I've constructed in my bookmarks. And related, option to flatten the view (as it is now).
Option to order feeds by "has unread".
Option to order feeds by date of most recent post.
Open the sidebar with feeds unexpanded would be great, along with "expand all" and "unexpand all".
"Sticky" manual ordering, although the equivalent could be accomplished by preserving the browser hierarchy.
Most of us realize that including our pet options would tend to move Sidebar from "lightweight extension" to "completely new feed management system." Your call, obviously.
April 3rd, 2008 at 10:12 am
Wow! this is a revolutionary idea! Congratulations guy! you did a very special and amazing job!
Keep up!!!
April 23rd, 2008 at 7:28 am
I'm here via Google to find out how to get rid of "open all in tabs". All around lamest and most nerve-racking "feature" in a web browser by far. Any help?
April 27th, 2008 at 8:40 am
keep up the good work
May 2nd, 2008 at 8:09 am
Great extension, but to my opinion it would need a small improvement : a toolbar button to mark only the selected feed as read. i like to do a first selection regarding the titles, and having to do a right click and select it for dozens of feeds every time is quite annoying... With that button added, this addon would appear to me as one of the best ever. Congratulations and thanks a lot !
May 2nd, 2008 at 5:37 pm
well done , it's really light and faster than other feed readers
May 14th, 2008 at 4:31 am
Hi,
Thanks for this addon it looks nice, but It has problem with Arabic language
it can't show any Arabic text, and some sites like this:
http://www.syria-news.com/sportnews.xml
has summary but it doesn't show it ,it works with Thunderbird.
so please add Arabic support and fix the summary problem.
regards,
Usama Akkad
May 15th, 2008 at 3:27 am
[...] Feed Sidebar Affiche les RSS à gauche. [...]
May 16th, 2008 at 1:48 pm
Dunno if this is a general chrome issue or not, but the bottom feed detail window seems to be setting the bg color to white but assuming the text color (which in my case is gray), giving me something not easy to read.
Also, for an extra, see if you can give me a sort issue. The bookmark folders let me sort the order of the feeds, but I'd have to manually reorder them to get them to show alphabetically in your panel.
May 21st, 2008 at 9:11 pm
Agree with request that #31, Lucile makes: toolbar button to mark selected feed as read. Failing that possibility, how about re-ordering the items in the context menu to put "mark feed as read" as the first item listed, delete "mark all as read" since that has a toolbar button already, and by all means delete the option to open everything in tabs!! Again, that has a toolbar button, and I nearly had the problem that others have mentioned about clicking it by accident. Scary!!
May 21st, 2008 at 9:26 pm
And another thing - #7 asks about listing the name of the feed in the sidebar the same way it was named when being subscribed to. I agree. It would be great if I could edit the name - could that option be added to the context menu or be put in somewhere else in some way, with minimal hassle to you, the programmer?
May 23rd, 2008 at 8:16 am
How to import sage feeds?
May 24th, 2008 at 12:29 am
How about notifications for new feed updates?
May 26th, 2008 at 7:01 am
Just checked this out, love it! I've tried other feed extensions in the past but most of them broke/tried to reinvent live bookmarks, which is a very bad idea.
My wishlist:
* Don't expand all folders by default, the list gets unwieldy. I'd rather have an accordion (only one folder open at a time) or separate panes for feeds and items.
* Yes, get rid of that "open all in tabs" button, it's insane. (Instead there could be an option to select several feeds and open by right-click.)
* favicons for the folders
* toolbar button!
* option to sort/filter by bookmark folders and tags
May 28th, 2008 at 2:49 am
Sorry, my English is not so good.
I have a problem / question.
The Add On "Free Sidebar 2.1.1" kompatiebel is with" FireFox portable 2.0.0.14"
I have not can be used Free Sidebar 2.1.1 installed however it.
In the activation of Free Sidebar, no RSS messages appear. Also can be added no installed bzw. Also no addresses can be called.
Is a certain free memory location need terminate functioned that it???
Have on my USB stick only 3.4 MB free.
Greeting Peter
May 28th, 2008 at 10:02 am
absolute shit compared to Maxthon 1/2 implementation of an RSS feed sidebar!
where is even the mini preview at the bottom to see what new entries are on each feed.. crap addon worse than sage rss
May 28th, 2008 at 10:05 am
Mark: It only shows new entries by default. Feel free to continue using Maxthon if it floats your boat.
June 1st, 2008 at 8:34 am
This is nice.. I wish you would have continued support for RSS Ticker, as I prefer tickers to sidebars, and InfoRSS is now broken, but c'est la vie.
Anyways I had a feature request: When hiding read items the last of the read items in a feed, could you have it not hide the feed? As it stands now I have to unhide all read items to be able to even see the feeds. I know it isn't a big deal, but when I don't see any feeds (because ive read all the articles) I panic and think the addon broke and ate it, so I'd like to be able to see the feed even if all of the articles have been read. Just my 2cents.
June 7th, 2008 at 1:39 am
Hi,
I am new to RSS. I've installed this add-on and I have a question. When I subscribe to a RSS feed, I am unable to locate the Feed Sibebar application in my computer.
Please help.
Thank you
RS
June 7th, 2008 at 5:36 am
how to add rss feed in this extension?
ansver this please also sorry my english.
June 13th, 2008 at 9:38 am
Nice program.
Would be great if you could add an option to default opening links in a new tab.
June 14th, 2008 at 4:45 pm
feedsidebar add-on it fail to install.
June 14th, 2008 at 7:35 pm
I tried to install the update and got an error message that said
"Firefox could not install the file at: https://addons.mozilla.org/en-US/firefox/addon/4869
because: Invalid file hash possible download corruption -261"
I also kept getting a message that feeds were not available after that happened and all of the feeds WERE available. Any fix for this?
June 16th, 2008 at 6:17 am
PLEASE add some way to sort the feeds other than the order in which they were added!
June 16th, 2008 at 9:12 am
They appears to be a problem with the latest FS v2.2.1
It will not update after installation of the update, Only recognizes it as FS v2.2 even on a clean profile ???
Help us please
Thanks
June 16th, 2008 at 7:58 pm
Wayney and ironside: It should be working now. There was a problem at Mozilla Addons.
June 17th, 2008 at 4:51 pm
Thanks for fixing it. I also would like to see a way of reorganizing the feeds (possibly off the Bookmarks Menu?), and also customizing the name of the feed. I have tried renaming the feed in my bookmarks, but i think it's pulling the name from the feed rather than the bookmarks. Thanks again for the addon.
June 17th, 2008 at 8:50 pm
Still problems as of 9:47pm June 17th.
Cannot get plugin with FF3 due to the following error.
Firefox could not install the file at
https://addons.mozilla.org/en-US/firefox/downloads/file/30701/feed_sidebar-2.2.1-fx.xpi
because: Invalid file hash (possible download corruption)
-261
June 17th, 2008 at 8:53 pm
LOL it worked when I clicked the above link.
Must be a problem with the FF site. Or the FF3 prog.
June 19th, 2008 at 7:01 pm
[...] Feed Sidebar 2.2.2 - Displays the items from your Live Bookmarks in the sidebar. [...]
June 20th, 2008 at 8:35 am
Very googd, 2.2!
June 20th, 2008 at 3:21 pm
Is there anyway to load my bookmarks from Google Reader into this Feed Sidebar? Is there a way to keep them synced?
June 21st, 2008 at 6:02 am
[...] Feed Sidebar - displays the items from your Live Bookmarks in the sidebar. [...]
June 25th, 2008 at 2:29 pm
Very cool add-on, thanks.
My situation may be rare enough that nobody cares to solve it.. but here goes.
The feeds I (want to) read are automatically generated by things like pmWiki recent change feeds and Bugzilla bug report feeds. The problem I have is that all of these are served over https, not http, and all require a login. Is there any chance Feed Sidebar could be made to remember my credentials, do the login negotiation and so forth before trying to update the feed? Alternatively, does anyone know a feed reader that can deal with this use-case?
Now, when the feeds try to update I either get "can't update" or "this isn't a feed" because the server is asking for credentials instead of just serving up the feed data. When I click on the view feed button in the error message in Feed Sidebar, I get about 4000 Firefox windows opening on my screen, each asking for a login for the single feed item they represent.
June 26th, 2008 at 7:20 am
Hi, is it possible to disable the ctrl+shift+f shortcut? It collides with developer toolbar addon... Thank you.
July 1st, 2008 at 1:48 am
I think there's an issue with memory management in Firefox when feed sidebar is running. I left my Firefox overnight with only two tabs open, plus the feed sidebar (which is set to check every 10 minutes), and the memory usage is 976 076 K....
July 7th, 2008 at 1:44 am
OK,
FS 3.0 not working very well in FF2.0.0.15
It doesnt seem to find all my live bookmarks for some reason and also afer a search i lose most of the found feeds from FS.
FS2.2.2 works perfectly so i dont know what the problem is hopefuullt you can fix it soon
Cheers
July 7th, 2008 at 1:49 am
Ooh, Almost forget... FS3.0 is also very slow in finding any feeds, If indeed it finds any!
Cheers
July 7th, 2008 at 5:56 pm
I would like to see an option to "Always open feed in new tab." I also notice that it seems to do a lot of disk thrashing when marking all as read. Other than those concerns, I think it's a great add-on and enjoy using it! :)
July 7th, 2008 at 9:03 pm
Great extension, well done! Only criticism I have with it is the performance of it. If there are a number of items in your feeds that you want to mark as read, it can take a good few seconds to iterate through them all to take them off the list. Similarly, checking feeds is very CPU intensive - 25% of my CPU time taken up on version 3.0.1, plus it "hangs" Firefox 3 whilst its doing this. I've done a complete removal of FF3 and reinstall, same problem.
July 7th, 2008 at 9:17 pm
i'm sorry i have to report a bug in the latest version i got today.
when u click on the site link in the side-bar, it wont open anymore.
July 7th, 2008 at 11:51 pm
As of FS 3.0, the Mark Read button on feeds (for the whole feed, not individual items in a feed) no longer marks the entire feed as read. I really liked the old functionality - it made it much easier to ignore entries that weren't of interest. Now I have to go through an individually mark each item as read, which takes too long.
July 8th, 2008 at 7:37 am
Please put an "Are you sure ?" option on Mark All As Read, or put an option in to not include on the context menu - prefer latter
I often select "Mark All as Read" when what I wanted was "Mark Feed as Read" - very annoying.
July 8th, 2008 at 2:27 pm
In response to the above suggestion: Oh please don't make it a confirmation (unless it has a "don't ask again" option)... :)
July 9th, 2008 at 9:02 pm
Thanks for the great extension!
Is it possible to have an option to put the sidebar on the right of the browser?
July 10th, 2008 at 2:06 pm
In addition to elipsoid's comment, the ctrl+shift+f shortcut also conflicts with feedbackfox.
July 15th, 2008 at 7:35 am
I was wondering if it is possible to have the following as options (it should not be very difficult):
* single click on an item to open the item not in the little preview at the bottom but instead on the browser (chrome://...) ;
* optional delete of an item ;
The first one should be very easy (just changing the double click to single click). I am not sure for the second one.
Thanks.
July 17th, 2008 at 1:54 pm
Great extension!
Just one little irritating bug: whenever i middleclick a link it opens it in a new tab (which is the expected behavior) but *also* displays the post very briefly in the lower preview area of the feedbar. The preview appears for like 0.3 seconds and then disappears again, which looks like an ugly flicker. rightclicking and selecting 'open in new tab' doesn't have this issue.
Using feedbar 3.0.1 on firefox 3.0
July 23rd, 2008 at 1:39 pm
There is some nasty bug in this extension:
I disabled ALL other add-on so I am 100% percent sure this is add-on is the cause
When I turn it ON and start firefox it take TWICE the memory compared to when running firefox without it
Also it tend to accumulate the mem leak as time elapses so after one day without stopping firefox I have a mem footprint as 500MB shared mem (290 resident)
This never happens if the add-on is not loaded.
This is on Linux and ff 3.0
Please make the addon eat less memory, it is very very good and I love it, but it renders all other tasks unsable after a few hours, when run on older laptops with less memory (like 512RAM).
July 30th, 2008 at 6:04 pm
Just an issue I've run across: Double clicking a feed item won't open it in the same tab. Also, selecting OPEN from the item's context menu will also not open it in the same tab. Nothing happens. I can, however, open in a new tab via either the middle-click, or via the context menu. Odd, double clicking worked for a few days so it must be some config change here. I've scoured about:config and cannot seem to find the problem. Can anyone steer me toward which options I should be looking at?
July 31st, 2008 at 2:39 pm
Just wondering if it's possible to display search results for items that have already been read when Hide read items is selected? At present I have to deselect Hide read items when searching to see all results.
July 31st, 2008 at 8:54 pm
In post number 76, I have figured out what was causing Feed Sidebar to fail responding to double-clicks. I thought I would share with the community by posting this solution...
In FasterFox extension, you must select CUSTOM to get at these other options!
Select the Popups tab, and un-check 'Disable Popups from Plugins'.
This does the trick, and Feed Sidebar once again responds to double-clicks!
I strongly suspect that enabling that option in FasterFox will break many other plugins too, luckily it is configurable!
July 31st, 2008 at 8:59 pm
In number 77 Karl asks if it is possible to disply search results for items that have already been read when 'Hide read items' is selected. According to my tests on two machines, the answer is no.
This would make a good option if a configuration dialog is added to the add-on. I hope the author will keep it in mind for a future update, it would be a real convenience to search for articles which have already been read -- probably the majority of searches would be to re-locate read items, so it really makes sense.
August 6th, 2008 at 9:56 am
Is there any way to change the order of the feeds? Ive changed the order manually in my live bookmarks folder, but the changes didn't carry through to FS. I even uninstalled and reinstalled FS, but it kept them in the old order. Surely there must be a way to change this.
August 7th, 2008 at 2:37 am
[...] Feed Sidebar - displays the items from your Live Bookmarks in the sidebar. [...]
August 7th, 2008 at 7:33 am
Fine add-on. There is only one feature that I miss: I would like to see the articles of the feeds that I subscribed all together in one flat list, simply ordered by date and time. To handle all those trees for my feeds (open this, close that, ...) is not very functional, I think.
August 7th, 2008 at 10:01 pm
An other request (but also an other thanks).
Many times when I see the short version of a blog, I just want to mark is as read, and go on to the next one. I can't find a key command to do that, which would be very handy. It could be the Delete key for example. Just a short cut for down-arrow followed by Right-click-mark-as-read on the previous read.
Thanks for the addon.
Frank D.
August 11th, 2008 at 5:08 am
How can i make feed sidebar show more than 10 items per feed?
August 12th, 2008 at 10:57 am
hi Christopher,
It would be great if you could add ability to show/hide feed sidebar by using pre-defined hotkey.
I'm sure that most people will agree with me that it would be really usefull.
Thanks in advance
-------
Regards
August 12th, 2008 at 10:59 am
Mathew: Ctrl+Shift+F does it.
August 12th, 2008 at 12:23 pm
hi Christopher
Thanks for your answer.
... and sorry - I didn't know about Ctrl+Shift+f ;)
August 14th, 2008 at 1:22 pm
I've dl the add-on but it's not registering any of my bookmarks, am I just an airhead, or is it an issue? Thanks
August 19th, 2008 at 5:43 pm
Hi, I've just updated to FF3 and I cant get the hotkey working, is there some option to enable it that I cant find?
August 24th, 2008 at 2:11 pm
Hi and Thank's for this add-ons.
Actually, I have the same comment as Zach (80).
Is there a way to re-order the feeds and not keeping the last one added at the end? Or is this future feature?
Cheers
August 24th, 2008 at 3:19 pm
Hi, great add-on.
But I really miss the "Mark All as Read" feature.
Used it a lot for bigger news feeds, why have it been deleted?
August 25th, 2008 at 5:06 pm
Thomas: You can still mark all as read by clicking the second toolbar button, or by right clicking below the list of feed items and selection "Mark All as Read."
August 26th, 2008 at 12:27 am
Thanks Christopher, I only read the changelog and I misunderstood it.
Great Add-On.
September 14th, 2008 at 3:18 pm
[...] Telecharger [...]
September 16th, 2008 at 7:38 pm
Hi, I've been using your addon for a while but it has started to create a very bad problem, it is causing my windows to "hang" for 5 seconds whenever I close them.
To explain more, whenever a firefox window is closed (i.e. one out of three open firefox windows) after clicking the X the window doesn't disappear but remains as if it has hanged. If I click on any other firefox window there's no reaction and if I forcibly minimize and restore the remaining windows they are white. All these happen for approximately 5 seconds then everything works fine. It doesn't happen when I close a tab inside the window.
I have verified it is a problem with this addon by disabling all others and enabling only it and getting the problem. When it is disabled of course the windows close immediately.
I am monitoring 25 blog feeds that are in the root of bookmarks. I wouldn't like to stop using your add on as it is really helpful!
September 17th, 2008 at 8:28 pm
good extension
in spanish please.
thanks.
September 18th, 2008 at 12:24 pm
Great add on! Its easy to use and much more reliable than Sage and Sage Too.
My only wish is that you could undo the "mark all as read" as numerous times I've accidentally clicked on it when I've been going form "mark feed as read".
September 22nd, 2008 at 8:04 am
Hi,
I am using the FeedSidebar 3.1 (with 15 feeds) and, in order to test the RSS feature of some forums, I set the "feed update frequency" option to 1 minute.
It finally turned out that, two days later, firefox was using 1.8 GB of memory.
I really think that there is a memory leak in this version.
Cheers,
Bruno.
September 23rd, 2008 at 5:10 am
Hi,
To continue on the memory leak subject, I've tested another Feed extension (same browser, same number of feeds), I also set its "feed update frequency" option to 1 minute and left my browser running 15 hours (instead of the 65 hours on the first test). The memory only "moved" from 135 MB to 143 MB.
I will try another test tonight using the Feed Sidebar that is definitely my favorite feed extension :-). Could you have a look please?
Cheers,
Bruno.
September 24th, 2008 at 2:26 pm
Hi,
Great extension!
I have 194 feeds and when I start Firefox Feed Sidebar stalls Firefox for minutes, this repeats itself about every 15 minutes.
Now Feed Sidebar reloads the same items, which is already marked as read.
One time Firefox suggested a should abort the Feed sidebar script - I turned off the warning, and the above behavior became the standard.
:-) Bo
October 8th, 2008 at 8:05 am
Hi,
I Agree with #62, #66 and #75 : This plugin is great but its memory consumption and hanging time really are disqualifying a daily usage.
Could you try to correct these before adding any new feature? Or else show us the code so that we could try to help?
Cheers,
adrien
October 17th, 2008 at 8:20 pm
could we have an option for "Confirm Unsubscribe", that if checked asks for conformation before doing the unsubscribe.
could we have a mark feed as read button, that would help reduce incidence of inadvertent unsubscribe actions.
and please take up the offers of help to resolve the performance issues.
TigerEyes
October 19th, 2008 at 5:52 pm
Great plugin, use it all the time. Couple of things though. I notice sometimes (update on open box unticked) that the feed bar doesnt update unless i open the sidebar manually.
Is it possible to have a confirmation on the open in tabs button as sometimes i have up to 200 links in the feeds, and if i click accidentally then it opens them all up. Its a pain closing them and i have a lot of tabs open already that i dont want to close.
Cheers, Keep up the good work :D
October 25th, 2008 at 1:27 pm
This is my favorite feed reader; however there are a couple annoyances. I would enjoy it much more if "Mark Feed as Read" was listed first in the context menu and/or there was shortcut to "Mark Feed as Read".
I like to read each feed at once, then I have to right click the feed and move down three spots on the context menu to mark the feed as read.
Something similar should be done to "Mark as Read" when you select on an individual headline.
By the way, I opened up the .xpi and fixed it myself, but it would be nice of it was officially done.
October 30th, 2008 at 2:57 pm
I love the sidebar, but the memory/cpu-thing is really an issue, especially when you have more than 5 feeds in the bar.
Is it possible to spread the load of checking the feeds, let's say update 1 feed at a time, every 10 minutes (orso).
Other than that, this is the best rss-reader I've used..
October 30th, 2008 at 4:22 pm
As mentioned in comment 105, I also have a CPU issue when the sidebar updates the feeds. The weird thing is, it was with the new update I just applied today that this issue started to appear, it was working fine before.
Hope you can work this out in the next update.
October 31st, 2008 at 5:12 am
Seems to be bug: Mark as read doesn't work in 3.1.4. Firefox version 2.0.0.17
October 31st, 2008 at 9:26 pm
Horrible CPU/Memory Hog issues. Running Vista here..Worked perfectly fine before the update as others have mentioned. Please fix it... Thank You!
November 1st, 2008 at 4:52 am
I also have "the" problem where Firefox totaly freezes during feed-update - rather annoying... I can also hear my HDD chew away like crazy during this freeze.
Looking forward to a fix to a, otherwise, great add-on!
Thanks!
November 1st, 2008 at 3:49 pm
Hey guys, I installed v3.1 from here https://addons.mozilla.org/en-US/firefox/addons/versions/4869#version-3.1 and it over-wrote the latest update, Firefox doesn't stall so horribly now. That's the best fix IMO until the developer has a chance to sort the mess from 3.1.4
Hope it helps someone.
November 1st, 2008 at 10:19 pm
Thanks Abdullah. Fixed it right up, for now.
November 3rd, 2008 at 1:02 am
How many RAM does this add-on use?
My poor laptop only has 700 MB , it seems to be a little slow ...
November 4th, 2008 at 11:41 am
The last update 3.1.5 doesn't work...
""
???
November 4th, 2008 at 11:42 am
The last update 3.1.5 doesn't work...
"----------------^command id="mark-all-as-unread" oncommand="window.parent.FEEDBAR.markAllAsUnread();" tooltiptext="&feedbar.markAllAsUnread;" /
"
???
November 4th, 2008 at 12:16 pm
XML Ayr??t?rma Hatas?: tan?mlanmam?? varl?kLocation: chrome://feedbar/content/options.xulLine Number 99, Column 5:
--------------------------------^
3.1.5 doesn't work..
November 5th, 2008 at 6:42 am
Hi Christopher.
After the last upgrade to 3.1.5. version, when I start "Feed Sidebar" I receive the following message:
"Erro no processamento de XML: entidade não definida
Posição: chrome://feedbar/content/sidebar.xul
Número da linha 25, coluna 3:
----------------^"
Do you have any ideia what is the problem? What should I do?
Thanks
Renê
November 5th, 2008 at 9:52 am
Rene: Sorry about that; version 3.1.6 is available now and it fixes this problem.
November 8th, 2008 at 11:42 am
You should put "Mark Feed as Read" at the top of the context menu or a keyboard shortcut. You should also allow each feed to have their own update time. That would make me feel so sexy.
November 9th, 2008 at 6:44 am
+1 to tommy. I already accidentally clicked on "unsubscribe" instead of "mark as read" once :(
I'd like to propose that you retreive the feeds async, not one after another.
Then you haven't to wait so long to see the new feed entrys when starting your browser(got nine feeds, a 16 MBit line, but it takes the sidebar more than 10 seconds to load nine feeds).
It also seems to me that the extension is blocks loading other home pages when starting firefox, maybe because of ff's connection limit.
Feel free to mail me if you want :)
GREAT WORK so far, btw!
November 26th, 2008 at 3:52 am
I'm having the problem with the feedbar choking when checking feeds as well. It gets to 21 of 32 feeds and then locks Firefox 3.0.4 for any where from a few seconds to several minutes. Eventually it will time out and say Stop Script or Continue.
December 3rd, 2008 at 10:13 pm
[...] Feed Sidebar [...]
December 23rd, 2008 at 11:52 am
At some point - either an upgrade of Firefox or enabling-disabling some other extenstion, the Feed Sidebar simply stopped being aware of updates. I can force the manual update and it says it updates my 14 feeds (their number grew in the meantime) BUT finds nothing new! although there surely is in Live Bookmarks shown. What could be the problem and, the main - remedy? Firefox 3.0.5, Feed Sidebar 3.1.6
December 23rd, 2008 at 11:54 am
Oh and it started yet with Firefox 3.0.4, update to 3.0.5 made no changes. I don't believe there were updates to Feed Sidebar since then, I watched for it, but cannot guarantee if it started with the last FS update or after (not earlier)
December 27th, 2008 at 4:43 am
Latest update (3.1.6) has broken a major feature. The option to only check feeds when the sidebar is open no longer has any effect - feeds are always checked at the configured interval irrespective as to the feed sidebar being pen or closed (Firefox 3.0.5). The only checking when the sidebar was open was a really good feature and I am pretty sure this problem was introduced with the latest update.
Otherwise a great extension (though without the above feature I will soon have to look elsewhere for a feed reader)
Ian
December 31st, 2008 at 6:25 pm
i have a bug report and a question.
the bug i've noticed is that it seems that if i've some unread feed items, open the new window, and then open the sidebar, the feed items don't show up, unless i reload them (in the second window). similarly, found feeds are forgotten when restarting browser. i don't think it would take much space to save the data and restore it after restarting browser, or would it?
the question i wanted to ask is: is there any way to share read feed history between computers, like you can share bookmarks using foxmarks? i find it pretty annoying that i have to mark the same feeds as read on different computers. it kinda makes me think about using google reader, despite the fact i dislike web apps.
January 9th, 2009 at 5:07 am
Hey Chris, the Sidebar looks nice, but for some reason I cant add new feeds. How do I do this?
January 16th, 2009 at 7:25 am
Re: refresh/update bug I described above - it is actually worse that that and not 100% consistent. When set to "only update what sidebar showing" it normally carries on and does its refresh anyway (every scheduled period, even when sidebar hidden the whole tme). However, when teh sidebar is showing it does not always do its refresh at the scheduled time. If anybody needs further info or details then please do ask back.
It is an excellent add-on but this bug is making the add-on pretty useless for me.
January 16th, 2009 at 11:08 am
I love this plug-in, I have been using for quite some time now, and as I suggestion, I would be really useful if beside each feed item (each new page) there would be a bookmark star so you can bookmark these items right form the bar for latter reading.
Thank you for this plug-in. :)
February 1st, 2009 at 1:59 pm
[...] Feed Sidebar [...]
February 5th, 2009 at 8:53 pm
Note - I've used Feed Sidebar for just a couple minutes...
It seems like a really great add-on.
===
Suggestions
= Filtering
I wish there was a way to allow filtering. And since I'm wishing - it would be nice if it allowed regex.
- filtering on the item's title
- filtering on the item's title url
- filtering on the item's body
= Manual Sorting
Feed Sidebar doesn't seem allow items to be sorted alphabetically. I assume automatically sorting things use a gigantic amount of memory. And iTunes like sorting "The ", "A ", "An " are ignored would be nice.
I've tried a zillion different methods - as far I can see filtering and sorting are the seemingly unattainable holy grail of feeds. If you ask anybody you love feeds - they'll tell you that the number one problem is information overload.
I've tried *everything* to filter and sort
- Google reader + Greasemonkey Google reader filter
- Thunderbird + built-in filters
- Every Firefox add-on related to live bookmarks.
All current methods to filter have lots of bugs, performance issues and other problems. Thunderbird has great potential - sorting is quick and painless - it allows filtering - but sadly it's crap as a feedreader. It has bug after bug (after bug).
A filtering and sorting example
I wrote a yahoo pipe to grab rss torrent feeds:
http://pipes.yahoo.com/pipes/pipe.run?_id=151725d78f0689d40bf3b1db1724c85a&_render=rss
Filtering on the "front end" - at yahoo pipes - would be a huge bug prone nightmare. Filtering on the "back end" - in my Firefox with Feed Sidebar having filter hits automatically marked as read would be a breeze. I really don't want items like "Overpaid Actor IV" or "Yet Another Awful Comedy" in my list.
Sorting should have been built-into live bookmarks from the beginning. My pipe can only sort with each "grab".
===
By the way - I like this feedback system.
1
I can assume my comments get read (and they aren't going into the void).
2
Comments can be read by all.
February 5th, 2009 at 9:06 pm
@ekbworldwide: There is some filtering in the sidebar; click on the right-most icon in the sidebar (the search icon), and you can enter a filter string in the textbox that appears. For example, typing
google
would only show entries where the feed title or feed items contain the term "google". Typing
"john smith" -computer -"screen door"
will only show entries that contain the phrase "john smith", but not the word "computer" and not the phrase "screen door".
February 6th, 2009 at 11:34 pm
[...] lot of people have asked for the ability to sort the feeds that appear in the Feed Sidebar extension for Firefox, so I've taken some time to integrate some basic sorting options. I would like to get some feedback [...]
February 12th, 2009 at 2:09 am
I was wondering if it was possible to implement a feature that gives the user the option of what to do when double clicking on the feed "folder" (aka feed title). Currently, double-clicking toggles the collapse/expand state for the feed. Personally, I'm interested in having your extension mimic the context menu's "Open Feed in Tabs" (for new posts) action when double-clicking, but I imagine having the other context menu options available for this feature might be helpful to others as well. Thanks for your consideration.
March 12th, 2009 at 2:58 am
Is this error generated from feedbar?
[Exception... "Component returned failure code: 0x80040111 (NS_ERROR_NOT_AVAILABLE) [nsIChannel.contentType]" nsresult: "0x80040111 (NS_ERROR_NOT_AVAILABLE)" location: "JS frame :: file:///usr/pkg/lib/firefox3/components/FeedProcessor.js :: FP_onStartRequest :: line 1440" data: no]
file:///usr/pkg/lib/firefox3/components/FeedProcessor.js
Line 1440
This error appears since when I've installed feedbar on firefox3.
Thank you in advace for you support.
Best regards, \fer
March 27th, 2009 at 2:03 am
[...] Feed Sidebar - Displays the items from your Live Bookmarks in the sidebar. [...]
April 2nd, 2009 at 3:32 am
Thank you for providing such a useful add-in to Firefox.
Would it be possible to use the delete key (not backspace) or another key, to mark a feed as read in the sidebar?
Regards,
Tom
April 3rd, 2009 at 8:59 pm
[...] been working on decreasing the CPU consumption of my Feed Sidebar Firefox extension; one of its main problems is that when it’s time to update the feeds, Firefox can grind to a [...]
April 6th, 2009 at 5:27 am
Just to be sure that it's not forgotten, I too have a serious problem with memory leakage, I tried updating to the new beta version but no luck. I'm using Firefox 3.0.8 on OS X 10.4
April 17th, 2009 at 5:02 am
[...] extension Feed Sidebar by Christopher Finke is a small extension that allows to view one’s Live Bookmarks in a [...]
April 28th, 2009 at 4:52 am
Great ad-on, I can't live without it. But just updated to Firefox 3.5 Beta 4 and it isn't compatible.
Please, release an updated version. Thank you very much for your work.
April 28th, 2009 at 3:33 pm
Great. But a few things you could change to make it even better.
1) I can't edit the name of the feed. I have to delete then add it and edit the name then.
2) I can't order the list in any way, to group selected items in alphabetical order of in categories.
3) I live-bookmark, in Firefox, the RSS feeds but some were showing twice in my bookmark folder. I deleted one from the folder and it vanished from the Sidebar. I added it back but it's still not showing up. I need some way of synching the feeds in the sidebar with the bookmarks in my firefox folder.
I'm using Xmarks (formally FoxMarks) - which is great, but perhaps this is confusing things? I'm not disabling it though, it's too useful!
Cheers!
April 29th, 2009 at 4:12 am
Another problem (not that my last comments have shown up here yet) is that 'mark as read' doesn't always work, either on the individual item or on the feed itself.
May 4th, 2009 at 8:09 am
Thank you, I love this extension except for one thing. I keep getting a box that says 'New Feed Item you have one new feed item' - at the top left of the screen and I can't get rid of it unless I restart the computer. It's driving me nuts!
May 12th, 2009 at 6:31 am
There seems to be a problem with the menu entry styling, the underline is "bonded" with the F letter.
http://www.upload.ee/image/77336/feeds.PNG
May 15th, 2009 at 8:35 pm
[...] was thinking it would be neat to add a recommendations component to Feed Sidebar. It would work like [...]
May 21st, 2009 at 10:43 pm
[...] Feed Sidebar The Feed Sidebar is an extension for Firefox that displays the items from your Live Bookmarks in the sidebar. [...]
May 22nd, 2009 at 5:23 am
Only some of the feeds are being displayed. I have 4 feeds but only three are displayed BUT the status bar says "scanning 4 feeds".
Any ideas?
June 16th, 2009 at 8:39 am
Thank you for providing a useful add-in to Firefox.
June 16th, 2009 at 11:44 pm
help my feed sidebar is broken. It claims to be checking feeds but no new posts are found ever. I've tried uninstalling the plug in and reinstalling it. Can't figure out what else to do. I have FF 3.0.11
June 20th, 2009 at 2:25 pm
Please add an option to open RSS with a simple left click mouse... Thanks
June 20th, 2009 at 4:46 pm
Hi,
Today I´ve updated the feed sidebar and I´ve noticed it reloads everytime I start firefox. This happened with the previous versions, but only if it was time to do so as I´ve programmed it on the update-time option. This slows the firefox start a lot, but there´s other annoying feature: when I close firefox every feed on the feed sidebar are deleted. Why does this happens? Is it a bug?
Thank you and congratulations for your work.
June 20th, 2009 at 9:57 pm
[...] Feed Sidebar – Feed Sidebar is a convenient way of reading RSS News Feeds. I have 26 tech-oriented web sites that I depend on for news happening in the tech world and a handful of personal blogs that I read as well. Visiting each site on a daily basis takes forever, so RSS feeds allow me to get the headlines very quickly and then allow me to choose which articles/posts I want to read. Feed Sidebar allows me to bookmark the RSS feeds right inside the browser and then just click on the headline to open the page, and I don’t need 2-3 windows open to do it. [...]
June 27th, 2009 at 5:32 pm
Is there a way to open links with just one click?
June 29th, 2009 at 6:49 am
Ever since the latest update to the Feed Bar my firefox has consistently crashed with a c++ runtime error. I have firefox 3.0.11 and your side bar 4.0.
June 30th, 2009 at 8:29 pm
The Addon is great. Is there a way to open links with just one left click mouse?
July 3rd, 2009 at 4:33 pm
I can confirm Kevins observation.
"Ever since the latest update to the Feed Bar my firefox has consistently crashed with a c++ runtime error. I have firefox 3.0.11 and your side bar 4.0."
July 3rd, 2009 at 8:19 pm
To open links with one left click: (Feed Sidebar 4.0)
Open with winrar:
Data\profile\extensions\feedbar@efinke.com\chrome\feedsidebar.jar
Then:
content\overlay.js
In line 1163:
Replace:
if ( event.which == 2)
With:
if ( event.which == 1)
July 6th, 2009 at 9:35 am
Another user with the "C++ runtime error" crash. It takes hours - I've never been at the computer when it happened - so probably a memory leak. Helpful, I know.
July 8th, 2009 at 2:19 pm
I switched to Feed Sidebar after Sage stopped working with 3.5, and I like it, the only problem is that it doesn't recognize feeds with URLs not ending in .rss. (like http://www.escapistmagazine.com/rss/articles/editorials/zeropunctuation) Could you fix this?
July 18th, 2009 at 7:04 am
Ever since FF 3.5 came out, Feedbar has been crashing on a regular basis and taking up a lot of memory (350MB working set with Feedbar vs. 170MB working set without Feedbar after 1H online / Server2008x64). Furthest I got before crashing was a whopping 1.6GB RAM taken before FF crashed again.
Don't get me wrong; this is by far the best RSS-tool for Firefox but atm very unreliable for me and taking precious resources while using Hyper-V for study-purposes (and thus needing a good amount of internet-pages as well).
July 24th, 2009 at 7:34 am
Leaks memory like a sieve. Memory usage goes up to 600 MB and more after a couple of hours, and I have maybe 20 feeds.
A good way to test this is set options to update only when the sidebar is open, start a fresh session with the sidebar closed. Then open the sidebar and watch memory usage go up. Also, feed updates use a ridiculous amount of CPU. The new version dances around this problem by spreading updates over time, but the underlying code is still extremely slow.
July 29th, 2009 at 4:38 am
other than the memory problem this is a five star got-to-have! The presentation is very clean and my grandmother can use it (if she knew what computers were..). It looks like countless months have been spent working on it!
Enough rave! thanks Chris!
July 30th, 2009 at 1:31 pm
Hello there,
really nice plugin.
Two improvements from my side:
- Several times I've already klicked on "Open All in Tabs" respectively "Open Feed in Tabs" unintentionally. As a result all the entries get marked as read. To set this back it would be nice if one is able to mark several entries and set them unread.
Generally the possibility to mark several items in combination with the usage of the context menue will be good.
- Is there a possibilty to add feeds manually?
I'm asking because I have a problem with the podcasts of the following site:
http://oe1.orf.at/podcast/
The XML-Links are not realized as RSS-feeds (e.g. http://static.orf.at/podcast/oe1/oe1_journale.xml)
Best Regards,
Jotun
August 14th, 2009 at 9:11 am
I have been running this with Firefox 3.0.13 and it just stopped working sometime since yesterday -- I click on the icon in my toolbar and nothing happens. The only thing that I've changed recently is that I installed the latest version of Java (jre6) this morning. Could this be the issue?
thanks,
jimbo
August 14th, 2009 at 9:39 am
Never mind -- working fine now!
September 10th, 2009 at 1:35 am
Hi Chris,
Great Extension! Also, just noticed that at least 3 of my must-have extensions are yours - great work! :)
In Feed Sidebar, you can set the "recency" by clicking the "clock" icon.
It seems you can also set this via "options", but "Only show items from the last X days", always stays at "1", even if you manually change it?
September 27th, 2009 at 10:19 am
For some reason, now that I've typed something in the search bar, it won't show all my feeds even after I've cleared the search. Everytime I open it back up, the search term is in the input. I clear it, nothing happens. Any ideas how to fix this?
November 26th, 2009 at 9:42 pm
@J: Same to me. Yet I just found a "temporary" solution for the showing problem: use BACKSPACE key instead of clicking X icon to clear the search bar.
November 30th, 2009 at 11:06 am
Anyone having problems with corrupted bookmarks ? Quite likely nothing to do with Sidebar, but I can not yet rule it out. Symptom is some of my most recently bookmarked sites (Ctrl-D) end up with just the 'name' (eg today "Overview - Training - Microsoft Office Online") but no URL or favicon anything else. They were there when I first saved the URL, but after restarting Firefox, only the name remains. Possibly relevant: I have a *lot* of bookmarks - not sure now to count, but my exported file is close to 10MB.
December 10th, 2009 at 12:01 am
[...] RSS Feeds gibt es hervorragende Erweiterungen für Firefox, z. B. Sage oder Feed Sidebar. Wenn Sie extra Programme bevorzugen, versuchen Sie es einmal mit GreatNews oder den Feedreader. [...]
December 11th, 2009 at 5:37 pm
When I right click on a feed and select open all in tabs, that feed's items are, indeed, all opened in tabs, but all other feeds are also marked as read (i.e. disappear from the sidebar). Am I misunderstanding something, or is this a bug?
Otherwise, this is a great add-on.
December 15th, 2009 at 6:14 pm
Well it seems that feed sidebar has become unreliable lately. I'm using v4.1.2 on FF 3.5.5, but it has been going on for a few weeks. Sometimes the feeds don't show up or with a delay of a day or so. But I think it has to do with the OS (Mac OSX), because FF on a Mac sucks, to be honest.
There's no pattern in which feeds show up and which don't do so (on time).